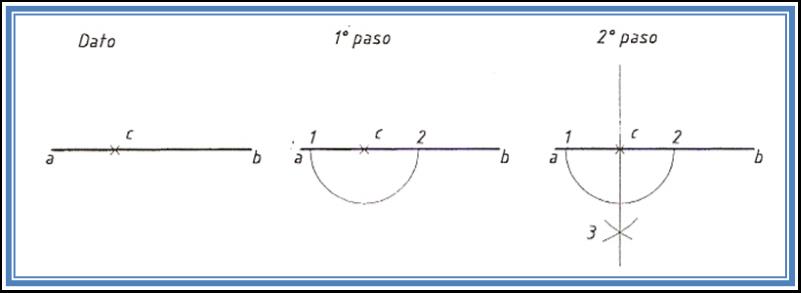
2) El punto c pertenece al segmento

Haciendo centro en c y con un radio cualquiera c1 trazamos una semicircunferencia que corte al segmento ab en los puntos 1 y 2. Haciendo centro en 1 y con un radio mayor que la mitad del segmento 1-2 se traza un arco haciendo centro en 2, se corta el arco anterior determinando el punto 3, se une 3 con c y se obtiene la perpendicular buscada.

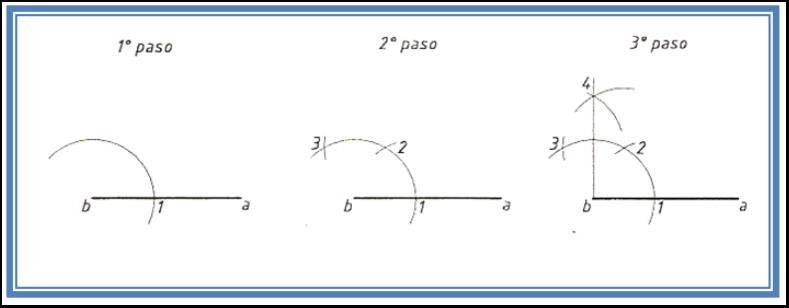
Perpendicular al segmento ab por el punto b

Para la construcción de la perpendicular al segmento por uno de sus extremos, en este caso el punto b, se traza un arco de circunferencia que corte al segmento dando como resultado el punto 1.

Con el mismo radio se hace centro en 1 y cortando el arco se obtiene el punto 2; desde este último se traza un nuevo arco dando el punto 3.

Entre estos dos puntos (2 y 3) se traza la mediatriz y obtenemos el punto 4; uniendo 4 con b obtenemos la perpendicular por el extremo del segmento.

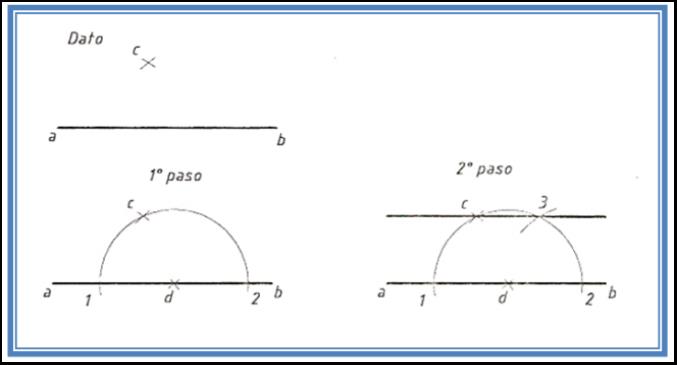
Paralela al segmento ab por un punto c

A) Haciendo centro en un punto inferior del segmento que llamaremos d con radio dc, trazamos una semicircunferencia de forma tal de cortar el segmento en los puntos 1 y 2.

Con centro en 2 y con radio 1c cortamos la semicircunferencia en 3. Uniendo c con 3 obtenemos la paralela al segmento ab.

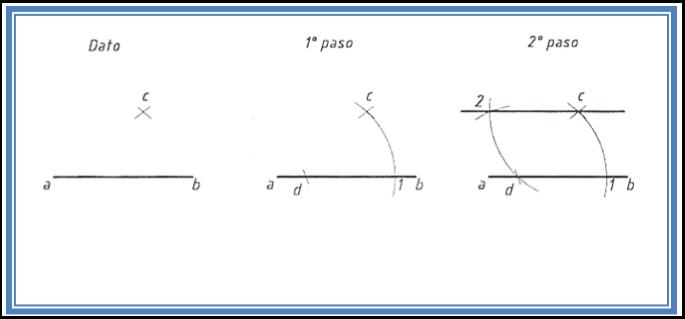
B) Dado el segmento ab se toma un punto cualquiera del mismo “d” Haciendo centro en él, y con radio dc, se traza un arco de forma que corte el segmento en el punto 1. Luego con el mismo radio pero haciendo centro en c, se traza un arco que pase por d. Por último tomamos la distancia de 1 a c y con centro en d, cortamos el arco antes mencionado, obteniendo el punto 2. Uniendo 2 con c se obtiene la paralela buscada.

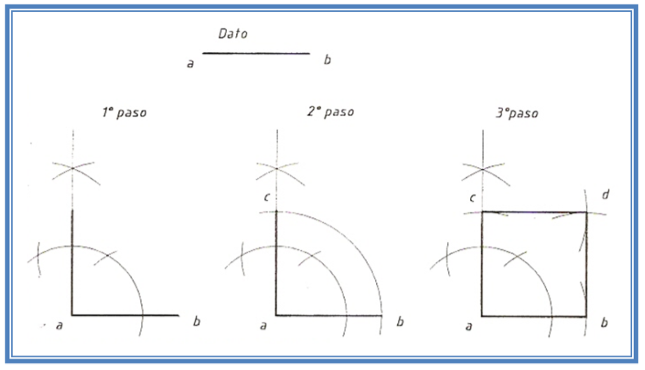
Dado un lado construir un cuadrado

 

Teniendo como dato el lado ab, trazamos una perpendicular por a, usando el método ya visto.

Con centro en a y con radio ab trazamos un arco que corte a la perpendicular obteniendo el punto c.

Con el mismo radio y con centro en c y en b trazamos dos arcos que al cortarse determinen el punto d.

Uniendo los puntos a, b, c y d con un espesor mayor nos queda definido el cuadrado.

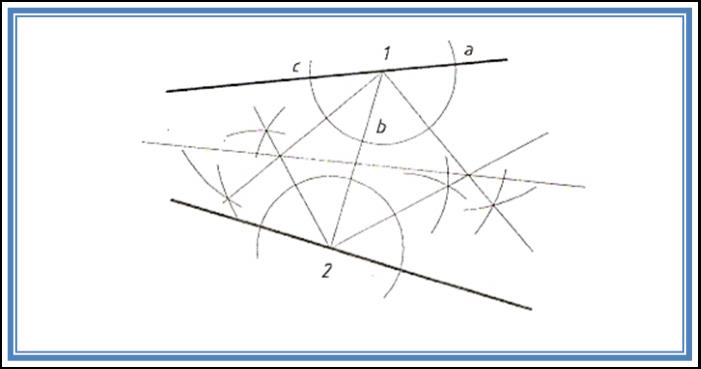
Bisectriz de un ángulo sin vértice

 

Se unen primeramente dos puntos cualesquiera, uno de cada lado del ángulo, con una auxiliar (por ejemplo puntos 1 y 2). Luego se traza un arco haciendo centro en cada uno de estos puntos, con cualquier radio, dando como resultado tres nuevos puntos (a_, b y c) por cada arco.  Tomando primero los puntos a y b, trazamos su bisectriz y tomando b y c trazamos otra bisectriz. Repitiendo este procedimiento con el arco del otro lado del ángulo, vemos que las bisectrices trazadas se interceptan dando como resultado dos puntos. Uniendo estos puntos obtenemos la bisectriz deseada.

Anterior

Siguiente